第一场认真补完的 CF,题目真的很好。
给你一个 n × m n \times m n × m ≥ 5 \ge 5 ≥ 5 ≥ 4 \ge 4 ≥ 4 1 1 1 0 0 0 n , m ≤ 400 n,m \leq 400 n , m ≤ 4 0 0
枚举矩形的左右边界,然后找一个最优的上下边界 l , r l,r l , r max l ≤ r { a l + a r + s r − s l − 1 } \max\limits_{l\leq r} \{a_l+a_r+s_r - s_{l-1}\} l ≤ r max { a l + a r + s r − s l − 1 }
求的长度为 n n n k k k m m m n ≤ 100 n \leq 100 n ≤ 1 0 0
将「所有包含这个数的区间中,不同的最大值的个数恰有 m m m m m m f i , j , k f_{i,j,k} f i , j , k i i i k k k j j j
考虑如何转移 f i , j , k f_{i,j,k} f i , j , k p p p p − 1 p-1 p − 1 i − p i-p i − p ( n − 1 p − 1 ) \dbinom{n-1}{p-1} ( p − 1 n − 1 )
跨越最大值的区间显然只会对不同最大值个数有 1 1 1 ( k − 1 ) (k-1) ( k − 1 ) c c c ( k − 1 ) (k-1) ( k − 1 ) j − c − [ k = 1 ] j-c-[k=1] j − c − [ k = 1 ] 1 1 1
所以有转移:
f i , j , k = ∑ p ( n − 1 p − 1 ) ∑ c f p − 1 , c , k − 1 ⋅ f i − p , j − c − [ k = 1 ] , k − 1 f_{i,j,k}=\sum_p \binom{n-1}{p-1}\sum_c f_{p-1,c,k-1}\cdot f_{i-p,j-c-[k=1],k-1}
f i , j , k = p ∑ ( p − 1 n − 1 ) c ∑ f p − 1 , c , k − 1 ⋅ f i − p , j − c − [ k = 1 ] , k − 1
时间复杂度 O ( n 5 ) O(n^5) O ( n 5 )
有 n n n i i i x i x_i x i y i y_i y i 1 ∼ m 1 \sim m 1 ∼ m n , m ≤ 2 × 1 0 5 n,m \leq 2\times 10^5 n , m ≤ 2 × 1 0 5
不难将题目转化为:将 i m o d p ∈ [ l , r ] i \bmod p \in [l,r] i m o d p ∈ [ l , r ] a i : = a i + 1 a_i := a_i+1 a i : = a i + 1
p > m p> \sqrt m p > m O ( m m ) O(m \sqrt m) O ( m m ) O ( m ) O(m) O ( m ) p ≤ m p \leq \sqrt m p ≤ m s i , j s_{i,j} s i , j m o d i = j \bmod i = j m o d i = j
时间复杂度 O ( n + m m ) O(n+m\sqrt m) O ( n + m m )
给你一个长度为 n n n a a a m m m m m m b 1 , b 2 , … , b m ∈ [ 1 , n ] b_1, b_2, \ldots, b_m \in[1,n] b 1 , b 2 , … , b m ∈ [ 1 , n ]
m ∑ i = 1 m a b i − ∑ i = 1 m ∑ j = 1 m f ( b i , b j ) m \sum_{i=1}^m a_{b_i} - \sum_{i=1}^m \sum_{j=1}^m f(b_i,b_j)
m i = 1 ∑ m a b i − i = 1 ∑ m j = 1 ∑ m f ( b i , b j )
其中 f ( l , r ) f(l,r) f ( l , r ) a a a [ l , r ] [l,r] [ l , r ] l > r l>r l > r l , r l,r l , r m ≤ n ≤ 4000 m \leq n \leq 4000 m ≤ n ≤ 4 0 0 0
不难发现式子可以化为这样:
∑ i = 1 m ∑ j = i + 1 m a b i + a b j − 2 f ( b i , b j ) \sum_{i=1}^m \sum_{j=i+1}^m a_{b_i} + a_{b_j} - 2f(b_i,b_j)
i = 1 ∑ m j = i + 1 ∑ m a b i + a b j − 2 f ( b i , b j )
观察到,若建出笛卡尔树,则 f ( b i , b j ) f(b_i,b_j) f ( b i , b j ) L C A ( b i , b j ) \mathrm{LCA}(b_i,b_j) L C A ( b i , b j ) a b i + a b j − 2 f ( b i , b j ) a_{b_i} + a_{b_j} - 2f(b_i,b_j) a b i + a b j − 2 f ( b i , b j ) d i s ( b i , b j ) \mathrm{dis}(b_i,b_j) d i s ( b i , b j )
故问题转化为,在带权的树上选出 m m m O ( n m ) O(nm) O ( n m )
一个 n n n m m m w x w_x w x x x x x ∈ [ 1 , n ] x\in [1,n] x ∈ [ 1 , n ] 1 1 1 x x x 1 1 1 x x x
有 q q q i i i w k i : = w k i + v i w_{k_i} := w_{k_i} + v_i w k i : = w k i + v i n , q ≤ 2 × 1 0 5 n,q \leq 2\times 10^5 n , q ≤ 2 × 1 0 5 m ≤ 3 × 1 0 5 m \leq 3\times 10^5 m ≤ 3 × 1 0 5
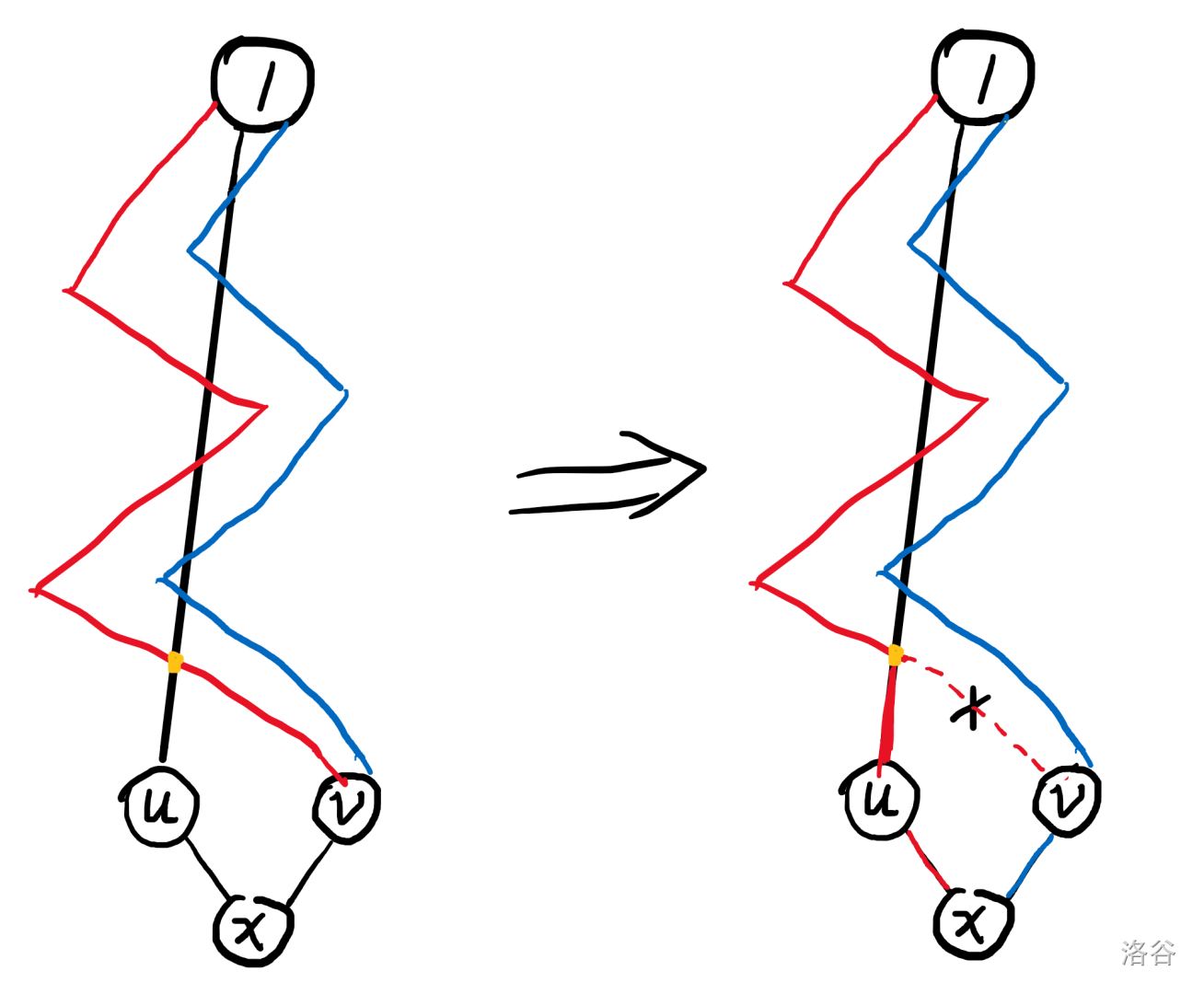
因为只有最短路相关的信息,故可以仅保留原图的最短路 DAG。同时,一条花钱加入的边 x → y x\to y x → y d y − d x d_y - d_x d y − d x d i d_i d i 1 1 1 i i i
然后考虑如何判定这个图是否合法:如果某个点只有一个入度,则一定不合法。所有点都有至少两个不同的入边(或者存在入边为 1 1 1
将点按照 d d d x x x x x x u , v u,v u , v 1 → u 1\to u 1 → u S S S 1 → v 1\to v 1 → v A A A B B B { A , B } \{A,B\} { A , B } S S S S S S S S S d d d S S S
这样就证明了图合法的充要条件:所有点都有至少两个不同的入边,或者存在入边为 1 1 1 u u u d x < d u d_x<d_u d x < d u u u u w x w_x w x
按照 d d d f i f_i f i s i s_i s i i i i w w w
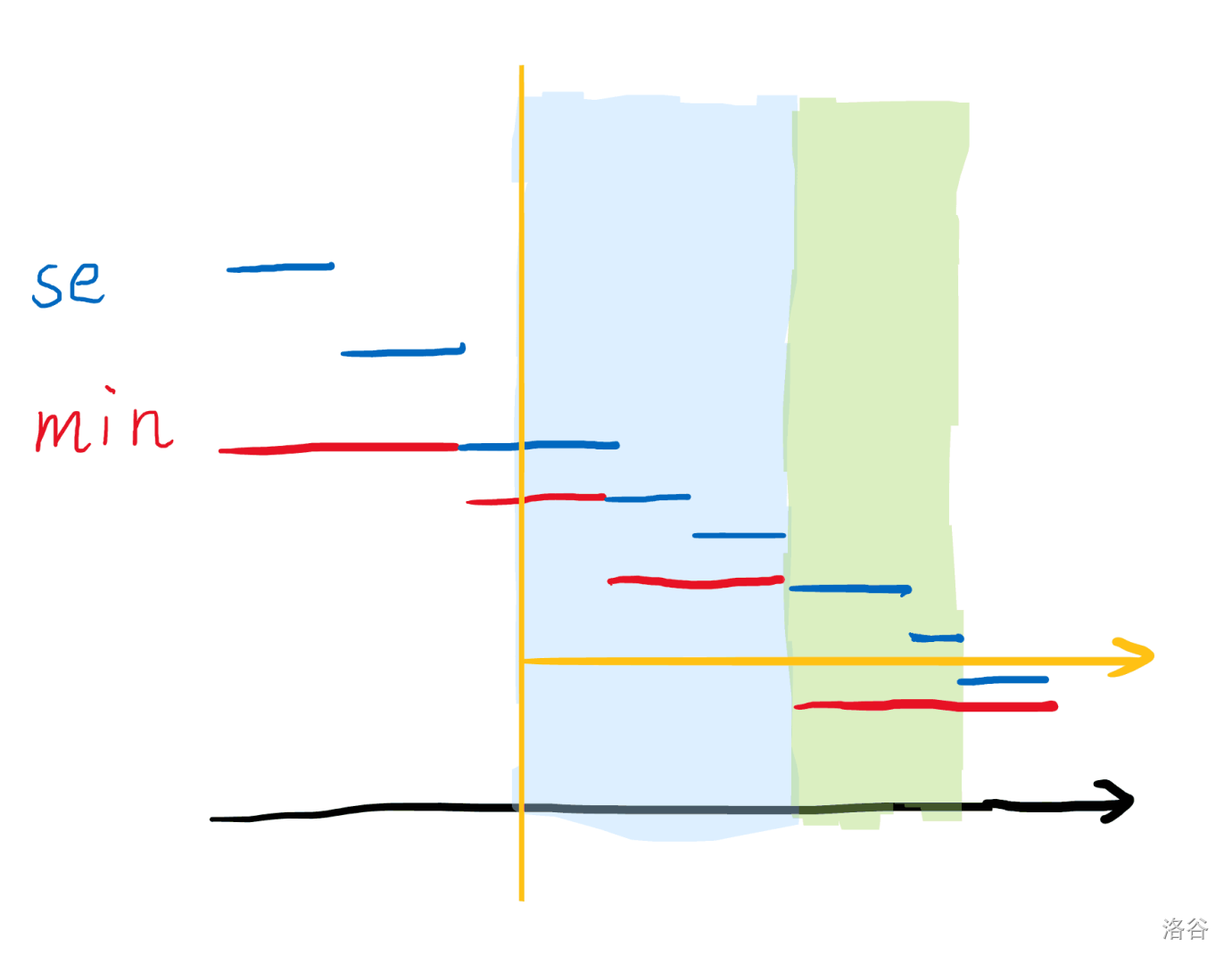
我们先讨论平凡的情况,也就是修改的既不是 f f f s s s f , s f,s f , s d d d m i n \tt min m i n s e \tt se s e x x x
受影响的区间有这两个:
在蓝色区间(x ≤ f x\leq f x ≤ f s s s f f f f f f x x x
在绿色区间(f < x < s f<x<s f < x < s s s s x x x
观察这两个修改的性质,不难发现可以令总势能为 f f f s s s h h h s s s h h h O ( n + q ) O(n+q) O ( n + q ) f , s f,s f , s f f f
加入特殊情况(修改的恰好是最小/次小值),这个均摊仍然满足吗?
修改次小值。显然,s s s f f f
修改最小值。乍一看似乎不满足均摊,但这样的修改并不会影响冲突(因为只是改了权值,并没有改编号),所以另外开一棵线段树维护最小值即可。
这样就做完了这道题,时间复杂度 O ( ( n + m + q ) log n ) O((n+m+q)\log n) O ( ( n + m + q ) log n )
一点细节,可能存在 d d d
求长度为 n n n 1 1 1 n n n < m <m < m 998244353 998244353 9 9 8 2 4 4 3 5 3 n ≤ 5 × 1 0 4 n \leq 5\times 10^4 n ≤ 5 × 1 0 4 m ≤ 1 0 9 m \leq 10^9 m ≤ 1 0 9
为方便表述,下文将用大写字母表示小写字母的 OGF,用 m / 2 m/2 m / 2 ⌊ m 2 ⌋ \left\lfloor\dfrac{m}{2}\right\rfloor ⌊ 2 m ⌋
将 < ⌈ m 2 ⌉ < \left\lceil\dfrac{m}{2}\right\rceil < ⌈ 2 m ⌉ S \tt S S ≥ ⌈ m 2 ⌉ \ge \left\lceil\dfrac{m}{2}\right\rceil ≥ ⌈ 2 m ⌉ B \tt B B
被分成若干个 S B S … B S \tt{SBS\dots BS} S B S … B S S \tt S S S \tt S S S B \tt SB S B
整个环是 S B \tt SB S B
先考虑第一种情况的计数,我们断环为链,统计由奇段拼成的链的个数。不妨长度为 i i i a i a_i a i i i i t i t_i t i T ( x ) = 1 1 − A ( x ) T(x) = \dfrac{1}{1-A(x)} T ( x ) = 1 − A ( x ) 1
环的断点恰好是奇段的断点,此时环等同于链,方案数为 t n t_n t n
否则我们枚举被断开的奇段的长度 i i i ( i − 1 ) t n − i a i (i-1)t_{n-i}a_i ( i − 1 ) t n − i a i
故 r e s = t n + ∑ ( i − 1 ) t n − i a i res=t_n + \sum (i-1)t_{n-i}a_i r e s = t n + ∑ ( i − 1 ) t n − i a i a a a
称相邻两个数(不含 1 1 1 n n n < k <k < k k k k ⌈ m 2 ⌉ \left\lceil\dfrac{m}{2}\right\rceil ⌈ 2 m ⌉ m / 2 m/2 m / 2 m m m f m , i f_{m,i} f m , i i i i m m m a m , i a_{m,i} a m , i a m , i = f m / 2 , i a_{m,i} = f_{m/2,i} a m , i = f m / 2 , i a m , 1 a_{m,1} a m , 1 f f f
序列和环的不同点在于,序列的首尾不一定是奇段:可能是开头形如 B S B … B S \tt{BSB\dots BS} B S B … B S S B S … S B \tt{SBS\dots SB} S B S … S B B S B … B S \tt{BSB\dots BS} B S B … B S B \tt B B S \tt S S B S \tt BS B S i i i b i b_i b i F ( x ) = B ( x ) 2 1 − A ( x ) F(x) = \dfrac{B(x)^2}{1-A(x)} F ( x ) = 1 − A ( x ) B ( x ) 2 B S B … S B \tt BSB\dots SB B S B … S B F ( x ) = A ( x ) + B ( x ) 2 1 − A ( x ) F(x) = A(x)+\dfrac{B(x)^2}{1-A(x)} F ( x ) = A ( x ) + 1 − A ( x ) B ( x ) 2 b m , i = f m / 2 , i b_{m,i} = f_{m/2,i} b m , i = f m / 2 , i F m / 2 F_{m/2} F m / 2 A m , B m A_m,B_m A m , B m F m F_m F m
因为 m m m F i F_i F i O ( log m ) O(\log m) O ( log m ) O ( n log n log m ) O(n \log n \log m) O ( n log n log m )
整个环是 S B \tt SB S B n n n g k g_k g k n n n m = k m=k m = k S B \tt SB S B a n s k ans_k a n s k m = k m=k m = k
我们发现将所有大数减去 ⌈ m 2 ⌉ \left\lceil\dfrac{m}{2}\right\rceil ⌈ 2 m ⌉ m / 2 m/2 m / 2 a n s m / 2 ans_{m/2} a n s m / 2 g k g_k g k + ⌈ m 2 ⌉ +\left\lceil\dfrac{m}{2}\right\rceil + ⌈ 2 m ⌉ + ⌈ m 2 ⌉ +\left\lceil\dfrac{m}{2}\right\rceil + ⌈ 2 m ⌉ g m = 2 ⋅ a n s m / 2 g_m = 2\cdot ans_{m/2} g m = 2 ⋅ a n s m / 2 r e s m res_m r e s m a n s m = r e s m + g m ans_m=res_m + g_m a n s m = r e s m + g m O ( n log n log m ) O(n \log n \log m) O ( n log n log m )
查看代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 #include <bits/stdc++.h> #define pbk push_back #define FOR(i,a,b) for(int i=a,i##i=b;i<=i##i;++i) #define ROF(i,a,b) for(int i=a,i##i=b;i>=i##i;--i) using namespace std;const int N=524293 ,mod=998244353 ,G=3 ,iG=(mod+1 )/3 ;inline int qpow (int a,int b) int R=1 ; for (;b;b>>=1 ,a=1ll *a*a%mod)if (b&1 )R=1ll *R*a%mod; return R; } inline int inv (int x) return qpow (x,mod-2 );}inline void chg (int & x) if (x>=mod)x-=mod;}int SZ,iSZ,R[N];void init (int S) for (SZ=1 ;SZ<S;SZ<<=1 ); iSZ=qpow (SZ,mod-2 ); FOR (i,1 ,SZ-1 )R[i]=(R[i>>1 ]>>1 )|((i&1 )*SZ>>1 ); } struct poly { int n;vector<int >a; int & operator [](int x){return a[x];} void siz (int x) resize (x,0 );} poly fit (int x) {return siz (n=x),*this ;} poly (int x=1 ,int A=0 ){n=x,siz (x),a[0 ]=A;} void ntt (int f) siz (SZ); FOR (i,0 ,SZ-1 )if (i>R[i])swap (a[i],a[R[i]]); for (int i=1 ;i<SZ;i<<=1 ){ const int w=qpow (~f?G:iG,(mod-1 )/i/2 ); for (int j=0 ;j<SZ;j+=i*2 ){ for (int e=1 ,k=0 ;k<i;e=1ll *e*w%mod,++k){ int &x=a[j|k],y=1ll *a[i|j|k]*e%mod; chg (a[i|j|k]=x-y+mod),chg (x+=y); } } } if (f==-1 )FOR (i,0 ,SZ-1 )a[i]=1ll *a[i]*iSZ%mod; } }; void Inv (poly f,poly& g,int D) if (D==1 )return void 0 ]=inv (f[0 ])); Inv (f,g,(D+1 )>>1 ); f.fit (D),init (D*2 ); f.ntt (1 ),g.ntt (1 ); FOR (i,0 ,SZ-1 )g[i]=(mod+2 -1ll *f[i]*g[i]%mod)*g[i]%mod; g.ntt (-1 ),g.siz (D); } poly Inv (poly f) { poly rs (f.n) ; return Inv (f,rs,f.n),rs; } poly operator +(poly x,poly y){ if (x.n<y.n)swap (x,y); FOR (i,0 ,y.n-1 )chg (x[i]+=y[i]); return x; } poly operator -(poly f){ FOR (i,0 ,f.n-1 )f[i]=mod-f[i]; return f; } poly operator *(poly x,poly y){ init (x.n+=y.n-1 ),x.ntt (1 ),y.ntt (1 ); FOR (i,0 ,SZ-1 )x[i]=1ll *x[i]*y[i]%mod; return x.ntt (-1 ),x; } poly operator -(poly x,poly y){return x+(-y);} int n,m,rs;poly solve (int m) { if (!m)return poly (n+1 ,1 ); poly F=solve (m/2 ),A (n+1 ),B (n+1 ,1 ); FOR (i,1 ,n)(i&1 ?A[i]:B[i])=F[i]; A[1 ]=(m+1 )/2 ; poly I=Inv (poly (1 ,1 )-A); F=A+B*B*I,rs=n&1 ?I[n]:(2ll *rs+I[n])%mod; FOR (i,3 ,n)rs=(rs+(i-1ll )*I[n-i]%mod*A[i])%mod; return F.fit (n+1 ); } signed main () scanf ("%d%d" ,&n,&m); solve (m),printf ("%d" ,rs); return 0 ; }
神题,神场,只能膜拜。
要是我退役之前能做出一道 E 或者 F 这样的题,就没有遗憾了。